바이트 값의 인코딩

아마 이 글을 보는 대부분은 논리회로를 배웠을 것이다.
숫자는 위와 같이 10진수, 16진수, 2진수로 나타낼 수 있다.
컴퓨터의 워드 길이

워드 길이는 정수값의 크기를 말한다. 요즘 컴퓨터는 대부분 64bit(8byte)이다.
이 때 하나의 정수의 주소는 메모리에서 한 덩어리(8byte)의 첫번째 위치이다. 따라서 연속된 워드의 주소는 4또는 8 바이트씩 증가한다.

32bit, 64bit, 48bit 컴퓨터에서는 각각의 자료형을 위와 같은 수의 byte로 표시한다.
Byte Ordering
가장 생소한 개념일 것이다.
컴퓨터마다 여러 바이트로 이루어진 데이터를 저장하는 순서가 다르다.
Sun, Mac, 인터넷은 big Endian,
x86, 안드로이드, ios, 윈도우를 실행하는 ARM 프로세서는 little Endian을 쓴다.
자 우선 중요한 바이트, 덜 중요한 바이트의 정의부터 잡아보도록 하자.
변수 x는 4바이트의 워드이고, 0x01234567이다. 한 바이트가 8bit이므로, 01/23/45/67 덩어리로 나뉜다고 볼 수 있다.
그럼 저 덩어리들 중에 가장 중요한 것과 덜 중요한 것은 어떤 덩어리일까?
아무래도 01이 가장 중요하다. 뒤로 갈수록 오차가 있어도 전체적인 값에는 영향을 덜 미치기 때문이다.
여기서 big endian은 가장 덜 중요한 byte가 최대주소에 저장되고,
little endian은 가장 덜 중요한 byte가 최소주소에 저장된다.
그럼 다시 위 예시에서 x의 주소가 0x100이라고 할 때

big endian은 큰 주소로 갈수록 덜 중요한 byte를 저장하고, little endian은 작은 주소로 갈수록 덜 중요한 수를 저장하는 것을 볼 수 있다.
자 그럼 직접 확인해보자.

다음과 같이 pointer과 전체 바이트 수를 넣으면 각 값과 주소를 출력하는 함수를 만들어두고

다음과 같이 a변수에 15213을 넣었다고 하자. 15213은 16진수로 0x00 00 3b 6d이다.
지금 출력된 것을 보면 주소가 작아질수록 덜 중요한 데이터가 들어가있는 것을 볼 수 있다.
따라서 해당 컴퓨터는 little endian 방식을 쓴다는 것을 알 수 있다.
비트수준 연산
비트연산자는 & | ~ ^가 있다. 정수형 연산자에 적용 가능하고, 인자들을 비트벡터로 처리하고, 비트들끼리 연산한다.
이 때 우리가 흔히 프로그래밍 언어에서 사용하는 &&와 &, ||와 |는 다르다는 것을 알아야한다.
&&, ||, !
이 경우는 전체가 참인지 거짓인지를 활용할 때 주로 사용한다.
0이면 거짓, 0이 아닌 건 모두 참이라고 처리한다.
연산의 결과는 무조건 0아니면 1이고, 만약 수식의 결과가 첫번째 인자를 계산해서 결정될 수 있으면 두번째 인자는 계산하지 않는다.
예를 들어, a&&a/5에서 a값이 0이 라면(거짓) 뒤에 a/5는 계산하지 않고, 바로 답이 거짓이라고 결론을 내린다.(뒤에값이 참이던지, 거짓이던지 전체 값은 항상 거짓이므로)
비트연산

비트단위의 연산은 위와 같다.
&는 두 비트 다 1일 경우에는 1을, 나머지는 0을 출력한다.
|는 두 비트 다 0일 경우에는 0을, 나머지는 1을 출력한다.
^는 두 비트가 같은 수를 나타내면 0을, 아니면 1을 출력한다.
~는 0인 비트는 1로, 1인 비트는 0으로 바꿔 출력한다.
쉬프트 연산
쉬프트 연산은 비트벡터를 왼쪽 또는 오른쪽으로 이동시키는 연산이다.
Left Shift : x << y
비트벡터 x를 왼쪽으로 y만큼 이동하는 연산이다. 이렇게 하면 왼쪽에 있던 비트들이 없어진다.
left shift는 한가지로, 왼쪽으로 y만큼 이동하여 생긴 오른쪽 비트의 공백은 모두 0으로 채운다.
Right Shift : x >> y
비트벡터 x를 오른쪽으로 y만큼 이동하는 연산이다. 이렇게 하면 오른쪽에 있던 비트들이 밀린만큼 없어진다.
right shift는 두가지로, 논리,산술 쉬프트로 나뉜다.
논리쉬프트는 왼쪽을 무조건 0으로 채운다.
예를들어 1100와 0011을 논리쉬프트로 왼쪽으로 하나 민다면, 0110과 0001이 된다.
산술쉬프트는 왼쪽 비트를 원래 가장 왼쪽에 있던 비트로 채운다.
예를들어 1100과 0011을 산술쉬프트로 왼쪽으로 하나 민다면 1110과 0001이 된다.
정수의 표현 방법
크게 두가지 표현방법이 있는데 unsigned int와 sigined int이다.
unsigned int
주어진 저장장소에 이진수로 표현한다. 부호가 없는 정수를 나타내서 모든 비트가 숫자를 표현하는데 쓰인다.
예를들어 BCD코드가 있다. 네 비트로 십진수 0~9를 표시한다.

이런식으로 한자리 한자리 표현하는 방식이다.
signed int
이건 부호를 갖는 수의 표현이다.
MSB에 의한 부호 표시는

이런식으로 맨 앞에 부호 표시를 하고 나머지 비트로 숫자 표시를 한다
이때 맨 앞 비트를 MSB라고 한다.
컴퓨터에서는 2의 보수로 부호형 정수를 표시하기로 정했다.(음수를 이런식으로 표현하기로 함)
비부호형 수에서 2의 보수형 정수로 변환하는 방법은 비트를 모두 뒤집고, 1을 더하는 방식이다.(모르면 논회 복습하고 오는거 추천)
정수의 인코딩
이진수로 되어있는 수를 정수로 인코딩 하는 방식을 알아보자
비부호형 정수의 경우

이런식으로 십진수로 변환한다.(흔히 우리가 하는 방식)
부호형 정수의 경우

이런 방식으로 변환한다.
가장 큰 자리는(2^(w-1)) 마이너스를 곱하고, 나머지 자리들은 더하는 방식이다.
아까 가장 앞 비트는 부호를 나타낸다고 했다. 만약 가장 앞 비트가 0이면 전체 값 중에서 음수가 없으니, 다 더하면 당연히 양수가 나온다.
하지만 가장 앞 비트가 1이면, 가장 앞 비트 값이 통째로 음수가 되고, 뒤 값들을 모두 더해도 이 값보다 작으므로, 음수가 나온다.
이렇게 말하면 이해가 안되니까 예시를 들어보자
-5를 만들어보자
5를 십진수로 표현하면 0101이다. -5로 만들기 위해서는 전부 뒤집고 1을 더하면 된다.
뒤집으면 1010, 1 더하면 1011이다.즉, -5는 2진수로 표현하면 1011이다.
1011에서 위의 방식으로 부호형 십진수로 변환하면 -8 + 0+ 2 + 1이 된다. 그럼 -5이다.
변환이 잘 되는 것을 확인할 수 있다.

위 과정은 15213과 -15113을 나타내는 이진수를 10진수로 바꾸는 과정을 설명한다.
양수의 경우, 부호를 나타내는 가장 앞 비트가 0이다. 즉, 1+4+8+32...를 다 해서 15213이 나온다.
하지만 음수의 경우, 부호를 나타내는 가장 앞 비트가 1이므로, 1+2+16+128.. -32768을 해서 -15213이 나온다.
정수의 표현 가능한 범위
비부호형과 부호형은 같은 비트수로 나타낼 수 있는 정수의 범위가 다르다
비부호형은 최소 0에서 2^w-1까지 나타낼 수 있다
하지만 부호형은 -2^(w-1)에서 2(w-1) -1까지 나타낼 수 있다. 양수 범위가 더 적은 이유는 맨 앞 비트가 0일 때는 모든 비트가 0인 0도 포함이기 때문

표로 한번 더 보자. 4비트가 있다고 했을 때 비부호형은 0부터 15까지(2의 4제곱인 16-1)표현 가능하지만, 부호형은 -8에서 7까지 표현 가능하다.
여기서 중요한 건 부호형에서 표현 가능 범위가 대칭형이 아니라는 것이다. 음수가 하나 더 많다.
그리고 회색으로 표시된 양수 부분은 부호형과 비부호형 모두 표현이 동일하다.
데이터 타입변환
c언어에서는 비부호형에서 부호형으로의 변환을 허용한다.

위와 같이 비부호형으로 변환했을 때, 양수는 변화가 없다. 하지만 음수의 경우 맨 앞 비트가 양수가 되무로, -15213이었던 값이 50323으로 변한다.

즉 다음과 같은 규칙으로 변환되는데, 기존 값이 양수라면 그대로 출력되고, 음수라면 기존 값에 2^w를 더한 값으로 변환된다.
이걸로 다시 설명해보자면
원래 -15213은 1+2+16+128..-32768을 해서 나온 값이다. 하지만, 이를 비부호로 변환하면 32768을 빼는 비트가 32768을 더하는 비트가 된다. 즉 두 값은 32768+32768값만큼 차이가 난다. 32768은 2^(w-1)한 값이었는데, 이거의 두배를 한 값의 차이가 나는거니까 부호형으로 변환할 때 2^(w-1)*2한 값인 2^w만큼 차이가 나는 것이다.
c언어에서의 타입변환
상수에서는 보통 아무것도 없으면 부호형 수를 나타낸다고 가정한다.
하지면 명시적으로 숫자 끝에 U를 붙이면(0U, 123U)수식 전체가 unsigned가 된다.
명시적 캐스팅

우리가 흔히 c언어에서 (long) 등등 로 타입변환 하듯이, 여기서도 괄호를 통해서 타입변환을 한다.
위의 방식은 명시적으로 타입변환을 하는 방식이다.
묵시적 캐스팅

이런식으로 부호형으로 선언된 변수에 비부호형 변수를 넣는 방식과 그 반대 방식으로 묵시적 캐스팅을 할수도 있다
하지만 이런 방식은 추천하지 않는다.
Casting 충격
한개의 수식에 unsigned와 signed값이 섞여있을 경우 모두 unsigned로 바뀌어 계산된다. 이는 비교연산자(<>=)에서도 발생한다.

여기를 보면 두 수 모두 부호형인 경우를 제외하고 모두 비부호형으로 바뀌어 계산되는 것을 확인할 수 있다.
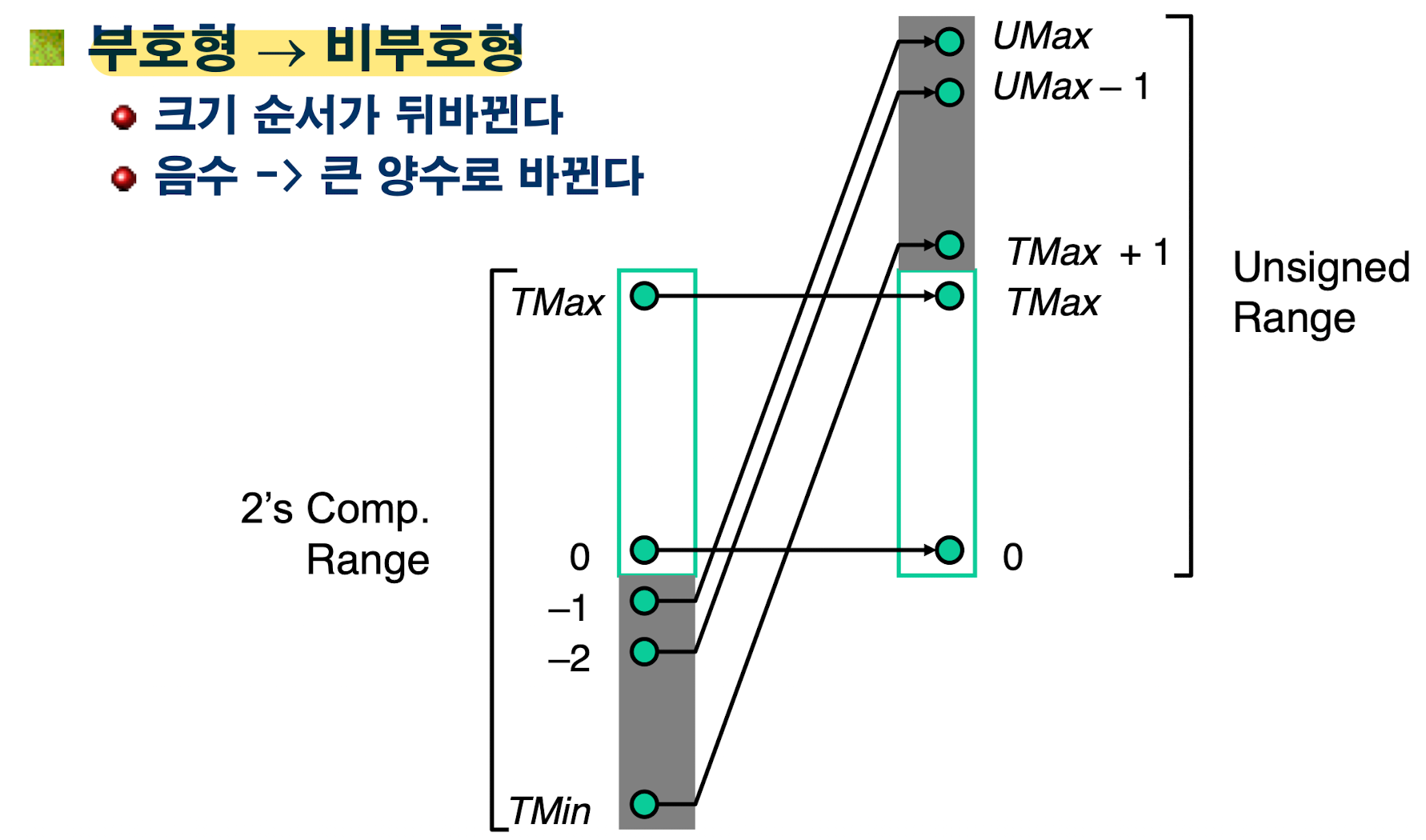
부호형이 비부호형으로 바뀔 때는 앞서 언급했듯이, 양수 부분은 그대로 바뀌고, 음수 부분은 기존 양수보다 더 큰 값으로 바뀐다.
정수의 연산
비부호형 덧셈
일반적인 덧셈 방식과 동일하다. carry(모르면 논리회로 고)는 무시한다.
이때 이런 방식은 mod 함수로 표시 가능하다. mod는 나머지로, c언어에서 %라고 생각하면 된다.
왜 이렇게 표현 가능하다고 하냐면
예를들어 011(3)과 101(5)를 더한다고 하자

그럼 1000(8)이 나오는건 당연하다. 근데 우리는 3비트만 표현 가능하므로 맨 앞 1은 캐리비트가 된다.
우리는 캐리를 버리니까 000만 나온다. 즉 답은 0이 나온다는 말이다. 이 0은 원래 정답이었던 8과 2^w인 8을 mod한 값이다(8나누기8의 나머지는 0이니까)

그래서 비부호형에서의 덧셈에서의 정답은 두 값을 더한 값에서 2^w를 나눈 값의 나머지라고 표현할 수 있다.
이해가 되지 않는다면 4(100)+5(101)를 한번 해봐라!
하지만 3+5는 0이 아니라 8이다. 이렇게 더한 값이 표현 가능한 비트 수(2^w-1)를 넘어갔을 때, 알맞지 않은 답이 나오는걸 오버플로우라고 한다.
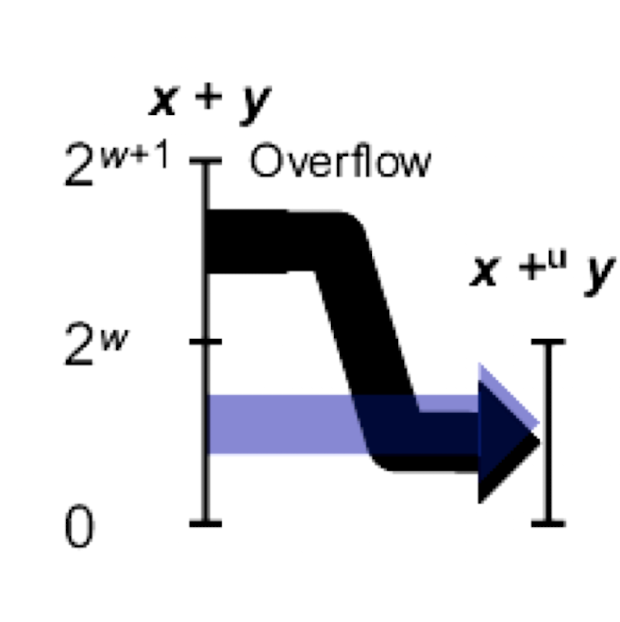
그래서 위의 그래프처럼 가능한 범위를 넘어가면 표현 가능한 범위 내로 수가 조정된다.(mod를 통해서라고 생각하면 쉬움)
부호형 덧셈
비부호형에서의 덧셈과 동일하게 수행한다.

즉 부호형인 u와 v를 비부호형으로 변환해서 더한 후, 다시 부호형으로 변환한 값과, 그냥 부호형 상태로 둘이 더한 값은 동일하다.
비부호형 덧셈에서 중요한건 오버플로우이다.

여기서도 마찬가지로, 덧셈을 했는데 표현 가능한 범위를 넘어가면 기존에 나와야 하는 정답값이 아닌 다른 값이 나오게 되는 오버플로우가 발생한다.
일단 위 표를 설명하자면, 앞서 설명했다시피 부호형에서 양수는 2^(w-1)-1까지, 음수는 -2^(w-1)까지 표현 가능하다. 표에서 이 범위 안에 있는 값들은 실제 결과에서도 동일하게 표시되는 것도 가능하다.
하지만 양수범위를 넘어간 값들을보면(PosOver) 음수 부분으로 변환되고, 음수범위를 넘어간 수(NegOver)는 양수로 변환되는 것을 볼 수 있다.
이걸 예를들어 설명하자면,
3비트까지 표현 가능하다고 했을 때, 011(3)과 010(2)을 더했다고 하자. 두 수는 첫 비트가 0이므로 양수이다.
3+2는 5이므로, 표현 가능한 양수 범위인 3을 초과했다.
실제로 이를 더하면 101이 된다. 첫비트가 1이 되었다. 즉 양수 두개를 더했는데 음수가 나왔다. 이런 경우, 오버플로우가 나왔다고 할 수 있다.
반대로 3비트까지 표현 가능한데 101(-3)과 110(-2)를 더했다고 하자.
-5는 음수 표현 가능 범위인 -4를 넘어간다.
실제로 이를 더하면 1011이 나온다. 맨 앞 비트는 캐리비트니까 버리면 결과값은 011이다. 011은 첫 비트가 0이므로 양수이다. 음수 두개를 더했는데, 양수가 나왔으므로 오버플로우가 발생한다.

따라서 음수끼리 더했는데 양수가 나왔거나 양수끼리 더했는데 음수가 나오면 오버플로우가 발생했다고 할 수 있는 것이다.
끝
출처
충남대 김형신교수님 시스템프로그래밍 강의자료
ESLAB | Home
Deep learning inference and training optimization for resource-constrained embedded systems
eslab.cnu.ac.kr
'CSE > 시스템프로그래밍' 카테고리의 다른 글
| [시스템 프로그래밍] 예외적인 제어흐름 - 프로세스 (1) | 2025.12.02 |
|---|---|
| [시스템프로그래밍] 실수의 표현 및 처리(1) (1) | 2025.10.21 |
| [시스템프로그래밍] 1장 컴퓨터 시스템 (2) | 2025.09.25 |
| [BombLab] 환경설정(맥북 사용자) (2) | 2024.10.06 |
| [BombLab] phase_6 해설 (2) | 2024.09.11 |



